股票作为现代经济中一种重要的融资手段正在被广泛的使用在商业以及个人投资领域。对于股票的甄别选自也有种类繁多的体系与理论。以前重要的两个派别是技术指标派和K线派,但随着近年来计算机的普及与性能的提升,通过编制特定的程序控制买卖时间点的量化交易派逐渐兴起。本文将以隐马尔科夫模型为判别模型,考察其在应用与股票投资上的适合性。
第一章 量化交易与隐马尔科夫模型
量化交易
股票作为现代经济中一种重要的融资手段正在被广泛的使用在商业以及个人投资领域。对于股票的甄别选自也有种类繁多的体系与理论。以前重要的两个派别是技术指标派和K线派,但随着近年来计算机的普及与性能的提升,通过编制特定的程序控制买卖时间点的量化投资派逐渐兴起。
量化交易的概念
量化交易是指以先进的数学模型替代人为的主观判断,利用计算机技术从庞大的历史数据中海选能带来超额收益的多种“大概率”事件以制定策略,极大地减少了投资者情绪波动的影响,避免在市场极度狂热或悲观的情况下作出非理性的投资决策。
量化交易的特点
定量投资和传统的定性投资本质上来说是相同的,二者都是基于市场非有效或弱有效的理论基础。两者的区别在于定量投资管理是“定性思想的量化应用”,更加强调数据。量化交易具有以下几个方面的特点:
- 纪律性。根据模型的运行结果进行决策,而不是凭感觉。纪律性既可以克制人性中贪婪、恐惧和侥幸心理等弱点,也可以克服认知偏差,且可跟踪。
- 系统性。具体表现为“三多”。一是多层次,包括在大类资产配置、行业选择、精选具体资产三个层次上都有模型;二是多角度,定量投资的核心思想包括宏观周期、市场结构、估值、成长、盈利质量、分析师盈利预测、市场情绪等多个角度;三是多数据,即对海量数据的处理。
- 套利思想。定量投资通过全面、系统性的扫描捕捉错误定价、错误估值带来的机会,从而发现估值洼地,并通过买入低估资产、卖出高估资产而获利。
- 概率取胜。一是定量投资不断从历史数据中挖掘有望重复的规律并加以利用;二是依靠组合资产取胜,而不是单个资产取胜。
量化交易的应用——算法交易
算法交易又称自动交易、黑盒交易或机器交易,是指通过设计算法,利用计算机程序发出交易指令的方法。在交易中,程序可以决定的范围包括交易时间的选择、交易的价格,甚至包括最后需要成交的资产数量。算法交易的主要类型有:
- 被动型算法交易,也称结构型算法交易。该交易算法除利用历史数据估计交易模型的关键参数外,不会根据市场的状况主动选择交易时机和交易的数量,而是按照一个既定的交易方针进行交易。该策略的的核心是减少滑价(目标价与实际成交均价的差)。被动型算法交易最成熟,使用也最为广泛,如在国际市场上使用最多的成交加权平均价格(VWAP)、时间加权平均价格(TWAP)等都属于被动型算法交易。
- 主动型算法交易,也称机会型算法交易。这类交易算法根据市场的状况作出实时的决策,判断是否交易、交易的数量、交易的价格等。主动型交易算法除了努力减少滑价以外,把关注的重点逐渐转向了价格趋势预测上。
- 综合型算法交易,该交易是前两者的结合。这类算法常见的方式是先把交易指令拆开,分布到若干个时间段内,每个时间段内具体如何交易由主动型交易算法进行判断。两者结合可达到单纯一种算法无法达到的效果。
小结
对于股票来说,一只好的股票由于不当的买入卖出时机亦有可能造成投资的失败或至少是盈利的减少。所以本文中并未按照量化交易的最基本出发点选股着手,而是着眼于对一只已选定的股票,什么样的买入与卖出时机能保证自己的盈利。即在本文中我们利用隐马尔科夫模型去模拟股价的一种潜在的涨跌区间交替关系,依此为根据决定股票的买入与卖出,控制了量化交易的时间选择,避免了人为选择的“追涨杀跌”等不理性行为,提高了风险规避能力,增加了机会找寻概率。同时,这样的控制存在着更加普适的意义,即无论什么样的股票都能增加盈利或者减少损失。
隐马尔科夫模型
过程或(系统)在时刻t0所处的状态为已知的条件下,过程在时刻t>t0所处状态的条件分布与过程在时刻t0之前所处的状态无关的特性称为马尔可夫性,而具有马尔可夫性的随机过程称为马尔可夫过程。
\[P(X(t_{n}) \leq x_{n}|X(t_{i})=x_{i})=P(X(t_{n}) \leq x_{n}|X(t_{n-1})=x_{n-1})\]对于一条马尔科夫链,我们通常只关注连续两个状态之间的转变,我们对链中从前一状态$s$转变为后一状态$t$的数学描述为:
\[a_{st}=P(x_i=t|x_{i-1}=s)\]对整个马尔科夫链$x$使用$P(X,Y)=P(X|Y)P(Y)$展开,由于马尔科夫性每个显示序列字符$x_i$出现的概率只与前一个字符$X_{i-1}$有关故我们可以将整个马尔科夫链化简如下:
\[\begin{equation}\begin{split} P(X)&=P(x_L,x_{L-1},···,x_1)\\ &=P(x_L|x_{L-1},···,x_1)P(x_{L-1}|x_{L-2},···,x_1)···P(x_1)\\ &=P(x_L|x_{L-1})P(x_{L-1}|x_{L-2})···P(x_2|x_1)P(x_1)\\ &=a_{x_{L-1}x_L}a_{x_{L-2}x_{L-1}}···a_{x_1x_2}P(x_1)\\ &=P(x_1)\prod_{i=2}^La_{x_{i-1}x_i} \end{split}\end{equation}\]在简单的马尔可夫模型(如马尔可夫链),所述状态是直接可见的观察者,因此状态转移概率是唯一的参数。在隐马尔可夫模型中,状态是不直接可见的,但输出依赖于该状态下,是可见的。每个状态通过可能的输出记号有了可能的概率分布。因此,通过一个HMM产生标记序列提供了有关状态的一些序列的信息。注意,“隐藏”指的是,该模型经其传递的状态序列,而不是模型的参数;即使这些参数是精确已知的,我们仍把该模型称为一个“隐藏”的马尔可夫模型。隐马尔可夫模型以它在时间上的模式识别所知,如语音,手写,手势识别,词类的标记,乐谱,局部放电和生物信息学应用。
由于“隐藏”的序列和我们能看见的序列之间的分离,我们需要一个桥梁来连接隐式序列中的状态k与我们可见的显示序列的字符b,为此我们定义了发射概率:
\[e_k(b)=P(x_i=b|π_i=k)\]由于隐式序列也满足马尔科夫性,所以每一个隐式序列状态只有关于它前一项状态且唯一发射一个显示字符,所以和马尔科夫链一样,我们同样可以拆分化简出一条显示序列$x$和一条隐式序列$π$的联合概率:
\[P(x,\pi)=a_{0\pi_1}\prod_{i=1}^Le_{\pi_i}(x_i)a_{\pi_i\pi_{i+1}}\]了解了隐马尔科夫模型的基本数学描述,科学家们提出了基于隐马尔科夫模型的三个问题与对应的算法:
解码问题: Viterbi算法
虽然在我们的隐马尔科夫模型中可以轻易地看到显示序列,但这个显式序列只是表面,它已经不再能表征出系统当前所处的隐藏状态。可令人不幸的是,这中不易被观测的隐式序列往往是我们真正想知道的。那么对于一条已知的显示序列,各种表示状态的隐式序列都有可能,只是他们发生的概率不同。那么对于所有的隐式序列$π$,我们自然会选择能使显示序列$x$有最大概率发生的作为我们推测的最有可能的隐式序列,即
\[π^*=\mathop{argmax}_πP(x,π)\]最可能的隐式序列$π^*$可以用过递归的方法求解得到。我们不妨假设最可能的隐式序列以观察值$x_i$结束于状态$k$,且其概率$P_k(i)$对所有状态$k$已知,那么可以用以下公式计算下一对应于观测值$x_{i+1}$的概率
\[P_i(i+1)=e_i(x_{i+1})\mathop{max}_k(P_k(i)a_{kl})\]所有的序列必须要以同一状态0(开始状态)为起点,因此初始条件即为$P_0(0)=1$,通过使指针不断回退,我们可以一步一步用回溯的方法来这道这条概率最高的隐式序列$\pi^*$,其伪代码逻辑如下:
- 初始(i=0):
- 递归(i=1···L):
- 终止:
- 回溯(i=1···L):
需要解释的是,此伪代码段假设存在结束状态,这也是为什么算式中出现$a_{kl}$。如果系统中并未对结束状态建模,那此项可以省略。另外一个值得注意的问题是下溢错误,这是由于在迭代计算时不断乘以了概率,而这些数字都是小于1的。这一问题在计算机中是十分严重的,通常我们会对连乘取对数,即$log(P_i(i))$,这样乘机将变成求和,使数字保持在一个合适范围,而这也正是本文采用的处理方法。Python代码实现如下:
def Viterbi(O,LM,CM):
LM = np.log(LM)
CM = np.log(CM)
pi=[[1,1]]
for i in range (1,len(O)):
pi.append([0,0])
if O[i] == "R":
pi[i][0] = LM[0][0]+max(pi[i-1][0]+CM[0][0],pi[i-1][1]+CM[1][0])
pi[i][1] = LM[1][0]+max(pi[i-1][0]+CM[0][1],pi[i-1][1]+CM[1][1])
else:
pi[i][0] = LM[0][1]+max(pi[i-1][0]+CM[0][0],pi[i-1][1]+CM[1][0])
pi[i][1] = LM[1][1]+max(pi[i-1][0]+CM[0][1],pi[i-1][1]+CM[1][1])
if pi[len(O)-1][0] >= pi[len(O)-1][1]:
H = "U";pr_H = "U"
else:
H = "D";pr_H = "D"
for i in range (len(O)-2,-1,-1):
if pr_H == "D":
if pi[i][0]+CM[0][1] > pi[i][1]+CM[1][1]:
pr_H="U"
else:
pr_H="D"
if pr_H=="U":
if pi[i][0]+CM[0][0] > pi[i][1]+CM[1][0]:
pr_H="U"
else:
pr_H="D"
H=pr_H+H
return H
评估问题: 前向算法
对于一条我们可以观察到的显式序列,除了关心其最有可能的隐式序列外,我们有时还希望知道这条显示序列出现的概率有多高。因为所有的隐式序列$π$都可以生成同一条显示序列$x$,这时我们必须把所有的可能隐式序列下出现此显示序列的概率求和,从而得到$x$的全概率
\[P(x)=\sum_πP(x,π)\]可又因为可能的路径$π$的数量随着序列的长度呈指数上涨,所以通过穷举所有路径强行计算上式是不现实的。考虑上一节中我们计算最优隐式序列$π^*$时的动态规划方法,我们发现了全概率的计算与这个方法十分相似,只要将算法中取最大值的步骤替换为求和即可,此方法被称为前向算法。
前向算法中与Viterbi变量$P_k(i)$对应的变量是
\[f_k(i)=P(x_1···x_i,π_i=k)\]这是$π_i=k$且显示序列结束于$x_i$的概率,递归方程为
\[f_i(i+1)=e_i(x_{i+1}\sum_kf_k(i)a_{kl})\]综上,归纳前向算法的伪代码段如下:
- 初始(i=0):
- 递归(i=1···L):
- 终止:
学习问题: Baum-Welch算法
(1)隐式序列已知时的估计
如果我们有幸获得一定量的训练集,即已知隐式序列的数据。此时我们可以对训练集中用到的每一个特定的状态转移或者发射统计次数,将他们记为$A_{kl}$和$E_k(b)$。于是我们可以得到训练集的$A_{kl}$和$E_k(b)$最大似然估计值分别是
\[a_{kl}=\frac{A_{kl}}{\sum_{l'}A_{kl'}}和e_k(b)=\frac{E_k(b)}{\sum_{b'}E_k(b')}\](2)隐式序列未知时的估计:Baum-Welch和Viterbi训练
而很多时候我们往往没有那么幸运,面对的训练集是不完整的,即只有那显而易见的显示序列。此时我们将不能用之前所说的简单计数的方法来得到最大似然估计值。但是,我们有特殊的方法应对这一棘手的问题,它被称为Baum-Welch算法。从自然含义上将这是一个分两步进行的迭代算法,首先任意给出一组$a_{kl}$和$e_k(b)$作为当前值,通过Viterbi算法计算出最优隐式序列$π^*$,然后回归到之前将的隐式序列已知时的估计,统计计数后得到$A_{kl}$和$E_k(b)$,然后计算得到新的$a_{kl}$和$e_k(b)$。迭代这一所述过程,直到$a_{kl}$和$e_k(b)$的变化小于设定的阈值时停止
可以证明,随着迭代过程次数的增加会使模型整体的对数似然值上升,因此该过程将收敛于一饿局部极大值。然而这局部最大值通常不止一个,终止于那个强烈依赖于我们第一次给出的初始参数猜测。特别是需要估计的HMM规模较大时,这个问题更加明显,在本文的最后也将提到此问题给我带来的极大困扰。其伪代码实现如下:
- 起始:
- 任取模型参数$a_{kl}$和$e_k(b)$
- 递归:
- 将所有的A和E变量设置于他们的伪计数$r$(或0)
- 对每条序列$j=1···n$:
用前向算法对序列$j$计算$f_k(i)$
用后向算法对序列$j$计算$b_k(i)$
将序列j的贡献添加到A和E中
- 计算新的参数模型
- 计算模型的新对数似然
- 终止:
- 如果对数似然变化小于某个设定的阈值
- 如果迭代次数超过最大值,则终止
第二章 实验结果与讨论
本文通过隐马尔可夫模型,对输入的股票显式序列进行建模从而得到推测的隐式序列。对于股票的显式序列有两种来源:一是通过股价的布朗运动规律,自动随机生成人造股价波动。第二是从雅虎财经上下载上证50的股票从上市到2018年4月25日的所有股价数据。以此为两种原始数据来源构建统一格式的股价显式序列,即如果当日收盘价大于开盘价则记录为“R”(red),反之记录为“G”(green)。
| 若收盘价-开盘价 | +0.13 | +0.21 | -0.43 | +0.54 | -0.22 | -0.23 | -0.11 | +0.02 | -0.05 |
| 记录的显式序列 | R | R | G | R | G | G | G | R | G |
模拟股价测试
基于几何布朗运动的人工股价随机函数
对于人工股价随机函数,这里用到几何布朗运动ln(S(y+t)/S(y))~N(mu,sigma),此处我们取时间t为一天,表示连续两天股价之比的对数值满足高斯分布。于是所得代码如下:
import matplotlib.pyplot as plt
import numpy as np
def Price(f=0.02,u=0,t=200):
v = f*np.random.randn(t)+u
P=[1]
for i in range (t-1):
P.append(P[i]*np.exp(v[i]))
plt.plot(P)
plt.show()
return P,v
\#价格水平通道曲线
Price()
\#价格上升通道曲线
Price(u=0.01)
\#价格下降通道曲线
Price(u=-0.01)
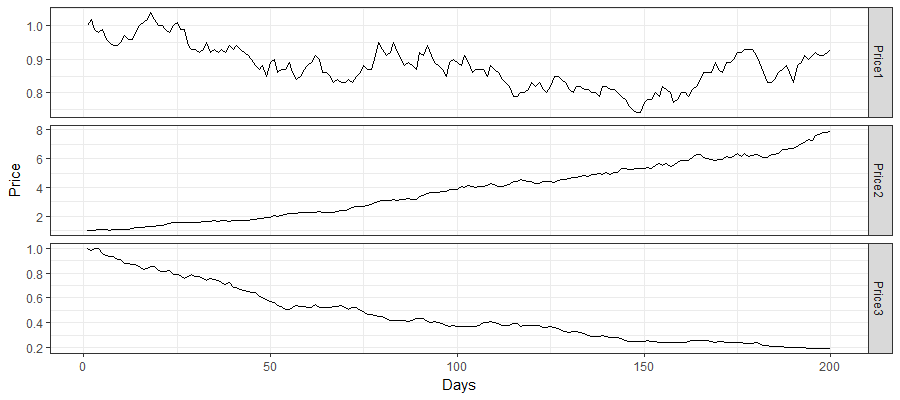
函数Price(f,u,t)中的f表示波动程度,默认为2%;u表示偏移量即表征了服从的高斯分布的均值大小,默认为0;t表示需要生成的股价天数,默认200天。依照编程函数生成的股价曲线如图1,从图中我们也可以发现其走势确实如我们所见的真实股票一样存在着波动,且随着u值的改变,改变了股价的走势。(出于美观性考虑此图由Python运行后的数据使用R中的ggplot做图)
隐马尔可夫模型简单测试
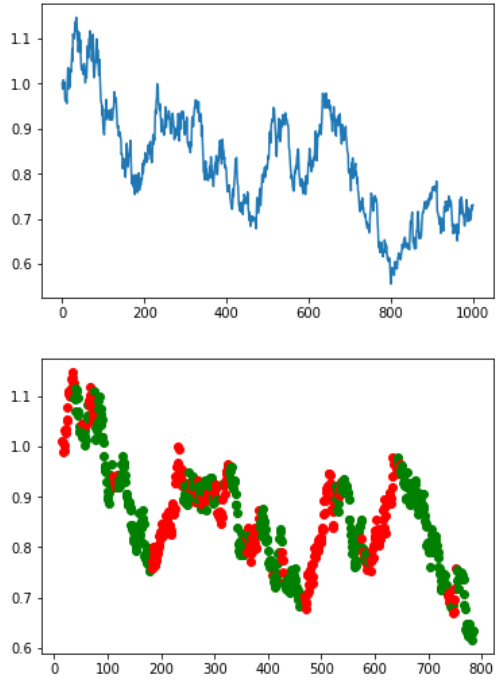
通过隐马尔可夫模型对我们上一步所说的基于几何布朗运动的人工股价随机函数生成的显式序列进行拟合,Viterbi算法推测所得的最大概率隐式序列可视化表示如上图。从图中我们可以发现,通过隐马尔可夫模型处理后的涨跌区间有着较好的拟合。在70-170天与650-800天这两段明显的下跌区间中甚至依旧可以找到一小段的回升,220-300天的震荡区间中也可以发现明显的上涨下跌交替出现的情况。
小结
通过对人工生成的股价测试结果来看,隐马尔可夫模型存在这一定的可行性。对于一段不明确上涨或下跌趋势的波动区间能有效的识别出其隐藏的上涨下跌区间。在明显的下跌区间中能依旧能有效的识别出一小段上涨区间,且一段上下波动的区间中也会灵活的识别转换隐式状态。这以简单的测试说明了隐马尔可夫模型对于股价变化的识别有效,这为我们下一步继续对上证50真实数据进行进一步测试提供了保障。
上证50真实数据回测
首先,我们需要对所选数据做一个基本解释。我们所用的数据取自雅虎财经,由于沪市上市的所有股票较多,所以我们选取了比较代表这一股市的上证50成分股。由于上证50作为一个股市的衡量指数,其成分股存在变动,我们选择的是2017年01月06日发布的样本,其中信威集团(600485)未在雅虎财经中找到数据故换取2015年08月31日中发布的样本国电南瑞 (600406)。综上我们这次的上证50真实数据测试的股票集合如下表:
| 浦发银行 (600000) | 民生银行 (600016) | 中国石化 (600028) | 南方航空 (600029) | 中信证券 (600030) |
| 招商银行 (600036) | 保利地产 (600048) | 中国联通 (600050) | 同方股份 (600100) | 上汽集团 (600104) |
| 国金证券 (600109) | 北方稀土 (600111) | 国电南瑞 (600406) | 康美药业 (600518) | 贵州茅台 (600519) |
| 山东黄金 (600547) | 东方明珠 (600637) | 海通证券 (600837) | 伊利股份 (600887) | 中航动力 (600893) |
| 东方证券 (600958) | 招商证券 (600999) | 大秦铁路 (601006) | 中国神华 (601088) | 兴业银行 (601166) |
| 北京银行 (601169) | 中国铁建 (601186) | 东兴证券 (601198) | 国泰君安 (601211) | 农业银行 (601288) |
| 中国平安 (601318) | 交通银行 (601328) | 新华保险 (601336) | 兴业证券 (601377) | 中国中铁 (601390) |
| 工商银行 (601398) | 中国太保 (601601) | 中国人寿 (601628) | 中国建筑 (601668) | 华泰证券 (601688) |
| 中国中车 (601766) | 光大证券 (601788) | 中国交建 (601800) | 光大银行 (601818) | 中国石油 (601857) |
| 方正证券 (601901) | 中国核电 (601985) | 中国银行 (601988) | 中国重工 (601989) | 中信银行 (601998) |
对于这些股票,我们下载其从上市到2018年4月25日的每天开盘价与收盘价,如之前已叙述,通过转化价格差的数据变成显式序列,用隐马尔可夫模型得到可能的隐式序列,经过测试所得数据通过R做图汇总如下
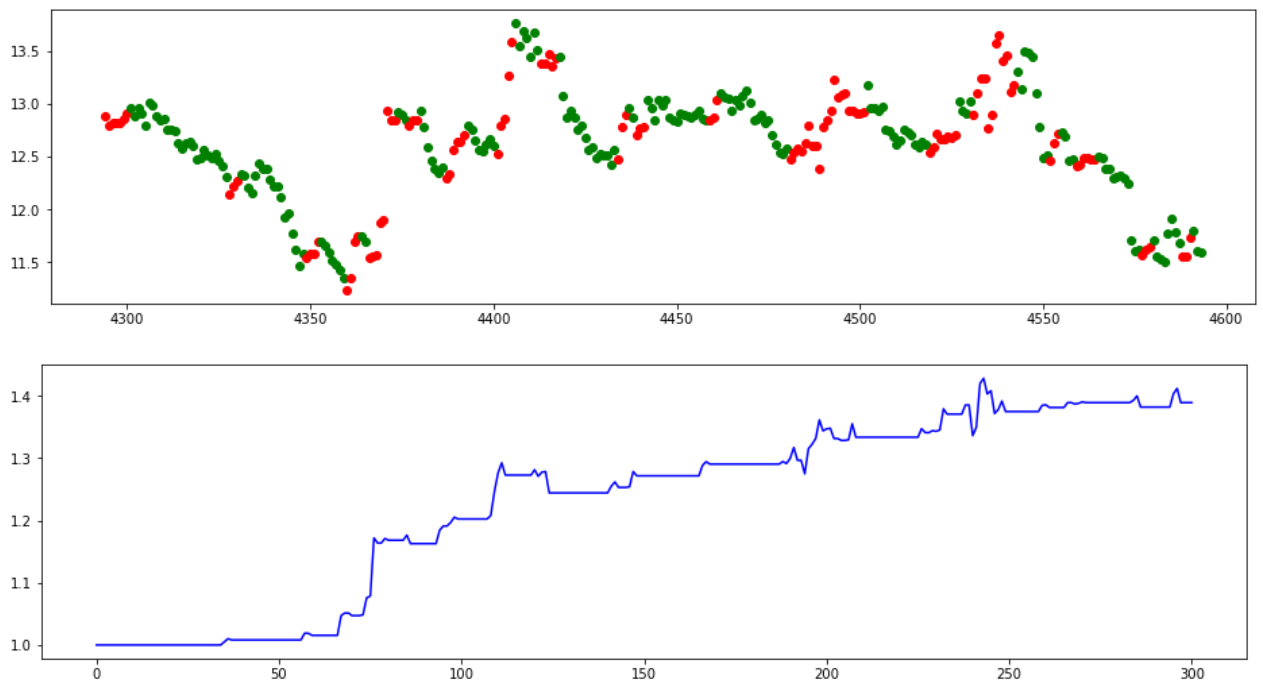
单一股票定时测试
我们选取浦发银行(600000)作为分析对象,如图中所示,我们采取的策咯是在上升区间转下降区间后卖出股票,在下降区间转上升区间后买入。由于信息滞后性,我们只有在出现转换后的第一天才知道转换的出现,因此我们将只有在转换出现的第二天买入或者卖出。即使如此,首先我们的模型有效的识别了上涨与下跌的区间,虽然在上涨区间中有下跌的错误识别但是对于整体一段上涨区间中结果依旧是上涨的;其次延后一天的投资依旧有可观的效果。对于本次测试我们选取的是最近300天的数据,最终虽然这一年的股票价格下跌了10%左右,但是运用隐马尔可夫建立的投资规则下投资可获得近40%的收益。
import csv
Data = []
with open('600000.csv','rb') as ff:
reader = csv.reader(ff)
for row in reader:
Data.append(row)
O = ""
Price = []
Rate0 = []
for i in range(len(Data)-2):
if(Data[i+2][4]!="null" and Data[i+1][4]!="null"):
Price.append(Data[i+1][4])
Rate0.append(float(Data[i+2][4])/float(Data[i+1][4]))
if (float(Data[i+2][4])-float(Data[i+1][4])>=0):
O = O + "R"
else:
O = O + "G"
import matplotlib.pyplot as plt
days = 300
Hdline = Viterbi(O,[[0.6, 0.4], [0.4, 0.6]],[[0.6, 0.4], [0.4, 0.6]])
fig, ax = plt.subplots(figsize=(16, 4))
for i in range (len(O)-days-1,len(O)-1):
if Hdline[i] == "U":
ax.plot([i],[Price[i]],'ro')
elif Hdline[i] == "D":
ax.plot([i],[Price[i]],'go')
plt.show()
\#图像化显示计算出的涨跌区间
fig, ax = plt.subplots(figsize=(16, 4))
Price_my = [1]
flag = False
for i in range (len(O)-days,len(O)):
if flag == False:
Price_my.append(Price_my[len(Price_my)-1]*1.0)
else:
Price_my.append(Price_my[len(Price_my)-1]*Rate0[i])
if Hdline[i-1] == "U" and Hdline[i] == "D":
flag = False
elif Hdline[i-1] == "D" and Hdline[i] == "U":
flag = True
ax.plot(Price_my,'b')
plt.show()
\#依照此涨跌去购买的收益曲线
单一股票时间变动测试
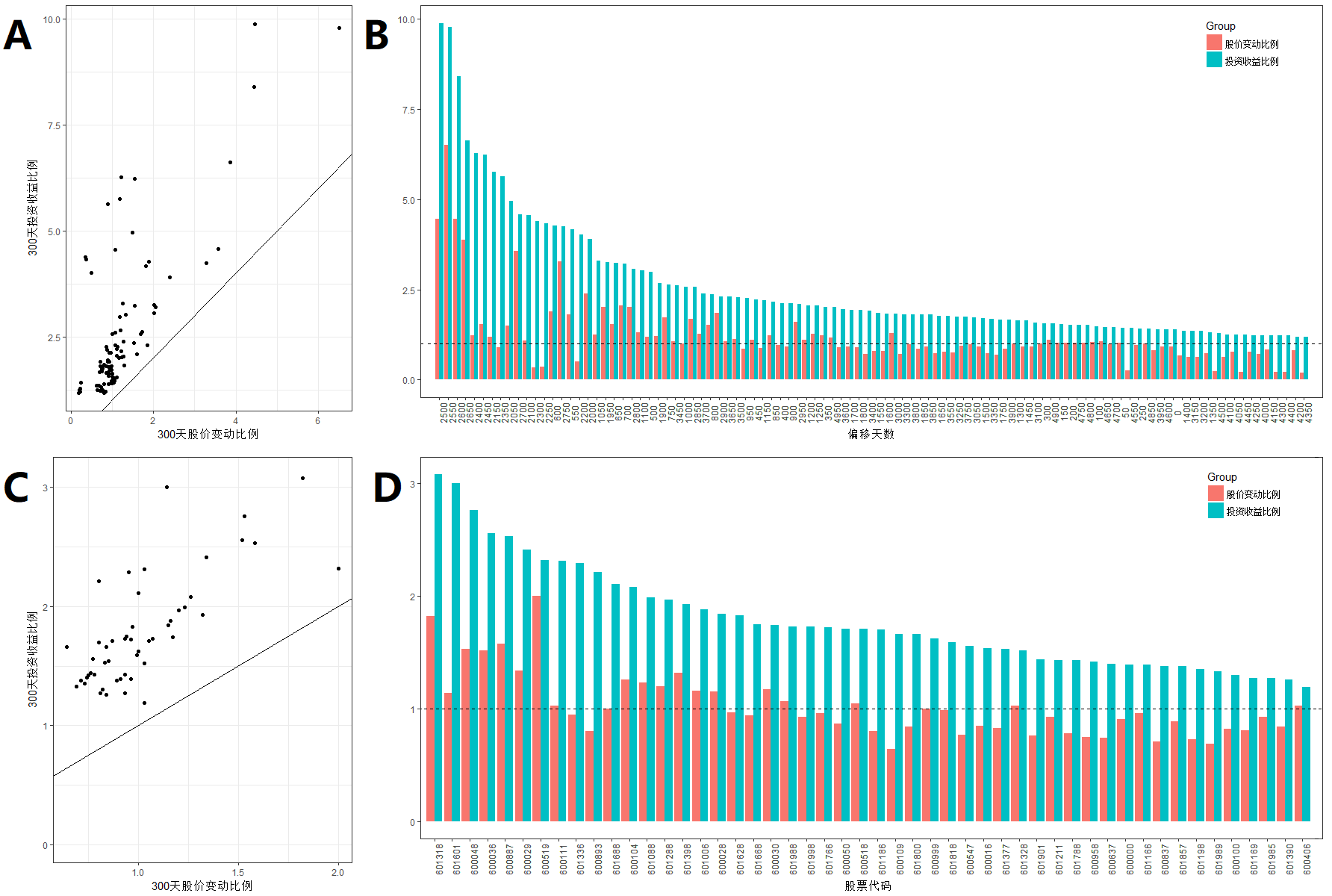
单个300天的小测试似乎不足以说明程序的有效性是否具有普遍的意义,于是我们继续拓宽被测试的时间取样。以300天为一个取样窗口,以最近300天为第一个取样窗口,每次向前滑动50天,共取样50组300天的数据进行如上一节所说的测试,计算出每组数据的投资收益与事实上的股票价格变动,如图A,B所示结果。图A中,横坐标为300天股价变动比例,纵坐标为300天投资收益比例,图中的直线表示在这300天结束时,投资收益等于实际价格变动时的情况,即无需任何操作,在开始时买入后持有300天卖出。我们可以发现所有的点均位于直线上方,这意味着当我们对一只股票持有达到300天时,使用隐马尔可夫模型决定买卖时机的投资策略总是优于直接持有300天。这一点很好的说明了本文所使用的方法有效地优化了我们的投资收益。其次B图中蓝色柱状表示我们的投资收益比例,而红色柱状表示的是实际300天后的价格变动,按照投资收益比例降序排列。图中的虚线表示的是投资收益比例为1的情况,即投资保本线。从图中我们欣喜地发现,虽然实际的股价变动在300天这一大的区间中不免有上下波动而出现亏损的情况,但是我们的投资收益比例无一例外的高于1,即盈利。这意味着在充分长的时间段内使用本文的方法,对于一直特定的股票来说,无论是什么时期,它不但能保证你的收益会优于直接持有改股票,而且几乎一定能保证正收益。
import csv
def F(x):
if x == 'U':
return 0
else:
return 1
def f(x):
if x == 'R':
return 0
else:
return 1
def right(O,Hdline,days,x):
t_num=0
f_num=0
for i in range(len(O)-days-x*50,len(O)-x*50):
if f(O[i]) == F(Hdline[i]):
t_num=t_num+1
else:
f_num=f_num+1
return float(t_num)/float(f_num+t_num)
def main(filename,x):
#print("%-15s %-15s %-15s %-15s"%("偏移天数","投资收益","实际涨幅","准确率"))
Data = []
with open(filename,'rb') as ff:
reader = csv.reader(ff)
for row in reader:
Data.append(row)
O = ""
Price = []
Rate0 = []
for i in range(len(Data)-2):
if(Data[i+2][4]!="null" and Data[i+1][4]!="null"):
Price.append(Data[i+1][4])
Rate0.append(float(Data[i+2][4])/float(Data[i+1][4]))
if (float(Data[i+2][4])-float(Data[i+1][4])>=0):
O = O + "R"
else:
O = O + "G"
Hdline = Viterbi(O,[[0.6, 0.4], [0.4, 0.6]],[[0.6, 0.4], [0.4, 0.6]])
Price_my = 1
flag = False
days = 300
for i in range (len(Price)-days-x*50,len(Price)-x*50):
if flag == False:
Price_my = Price_my*1.0
else:
Price_my = Price_my*Rate0[i]
if Hdline[i-1] == "U" and Hdline[i] == "D":
flag = False
elif Hdline[i-1] == "D" and Hdline[i] == "U":
flag = True
print("%-11.6s %-11.2f %-11.2f %-11.2f"%(x*50,round(Price_my,2),
float(Price[len(Price)-1-x*50])/float(Price[len(Price)-1-days-x*50]),
right(O,Hdline,days,x)))
print("%-15s %-15s %-15s %-15s"%("偏移天数","投资收益","实际涨幅","准确率"))
for i in range(100):
main('600000.csv',i)
| 偏移天数 | 投资收益 | 实际涨幅 | 准确率 |
| 0 | 1.39 | 0.91 | 0.77 |
| 50 | 1.43 | 1.03 | 0.77 |
| 100 | 1.48 | 1.05 | 0.78 |
| 150 | 1.54 | 1.03 | 0.81 |
| 200 | 1.53 | 1.02 | 0.81 |
| ··· | ··· | ··· | ··· |
| 4750 | 1.52 | 1.02 | 0.80 |
| 4800 | 1.51 | 1.03 | 0.81 |
| 4850 | 1.42 | 1.01 | 0.79 |
| 4900 | 1.56 | 1.11 | 0.80 |
| 4950 | 2.01 | 1.17 | 0.81 |
上证50样本300天测试
经过之前的分析测试,我们完成了本文方法对单一特定股票的适应性证明。现在我们拓宽股票池的选择,以上证50中的50只样本股作为测试目标,考察此方法对其他股票是否有一样的适配性,测试结果如图C、D。分析方法与上一节类似,从图C中我们不难看出即使是推演到50只不同的股票,图中收益比例与实际价格做出的点都在等价值线的上方,意味着对于不同的股票当我们对一只股票持有达到300天时,使用隐马尔可夫模型决定买卖时机的投资策略总是优于直接持有300天。而图D中所有的蓝色柱状都高于保本线,可见即使多余不同的股票,本文中的投资方法依旧有良好的保本性。这意味着在充分长的时间段内使用本文的方法,对于不同的股票都能保证你的收益会优于直接持有改股票,而且几乎一定能保证正收益。
def right(O,Hdline):
t_num=0
f_num=0
for i in range(len(O)-days,len(O)):
if f(O[i]) == F(Hdline[i]):
t_num=t_num+1
else:
f_num=f_num+1
return float(t_num)/float(f_num+t_num)
def result(f_list):
print("%-15s %-15s %-15s %-15s"%("股票代码","投资收益","实际涨幅","准确率"))
for i in range (len(f_list)):
main(f_list[i])
def main(filename):
Data = []
with open(filename,'rb') as ff:
reader = csv.reader(ff)
for row in reader:
Data.append(row)
O = ""
Price = []
Rate0 = []
for i in range(len(Data)-2):
if(Data[i+2][4]!="null" and Data[i+1][4]!="null"):
Price.append(Data[i+1][4])
Rate0.append(float(Data[i+2][4])/float(Data[i+1][4]))
if (float(Data[i+2][4])-float(Data[i+1][4])>=0):
O = O + "R"
else:
O = O + "G"
days = 300
Hdline = Viterbi(O,[[0.6, 0.4], [0.4, 0.6]],[[0.6, 0.4], [0.4, 0.6]])
Price_my = 1
flag = False
for i in range (len(Price)-days,len(Price)):
if flag == False:
Price_my = Price_my*1.0
else:
Price_my = Price_my*Rate0[i]
if Hdline[i-1] == "U" and Hdline[i] == "D":
flag = False
elif Hdline[i-1] == "D" and Hdline[i] == "U":
flag = True
print("%-11.6s %-11.2f %-11.2f %-11.2f"%(filename,round(Price_my,2),
float(Price[len(Price)-1])/float(Price[len(Price)-1-days]),right(O,Hdline)))
result(['600000.csv','600016.csv','600028.csv','600029.csv','600030.csv',
'600036.csv','600048.csv','600050.csv','600100.csv','600104.csv',
'600109.csv','600111.csv','600406.csv','600518.csv','600519.csv',
'600547.csv','600637.csv','600837.csv','600887.csv','600893.csv',
'600958.csv','600999.csv','601006.csv','601088.csv','601166.csv',
'601169.csv','601186.csv','601198.csv','601211.csv','601288.csv',
'601318.csv','601328.csv','601336.csv','601377.csv','601390.csv',
'601398.csv','601601.csv','601628.csv','601668.csv','601688.csv',
'601766.csv','601788.csv','601800.csv','601818.csv','601857.csv',
'601901.csv','601985.csv','601988.csv','601989.csv','601998.csv'])
| 股票代码 | 投资收益 | 实际涨幅 | 准确率 | 股票代码 | 投资收益 | 实际涨幅 | 准确率 |
| 600000 | 1.39 | 0.91 | 0.77 | 601169 | 1.27 | 0.81 | 0.80 |
| 600016 | 1.54 | 0.85 | 0.79 | 601186 | 1.70 | 0.80 | 0.75 |
| 600028 | 1.84 | 1.15 | 0.80 | 601198 | 1.35 | 0.73 | 0.73 |
| 600029 | 2.41 | 1.34 | 0.76 | 601211 | 1.43 | 0.93 | 0.78 |
| 600030 | 1.74 | 1.17 | 0.76 | 601288 | 1.97 | 1.20 | 0.83 |
| 600036 | 2.56 | 1.52 | 0.81 | 601318 | 3.08 | 1.82 | 0.77 |
| 600048 | 2.76 | 1.53 | 0.81 | 601328 | 1.52 | 1.03 | 0.79 |
| 600050 | 1.71 | 0.87 | 0.84 | 601336 | 2.29 | 0.95 | 0.78 |
| 600100 | 1.30 | 0.82 | 0.85 | 601377 | 1.53 | 0.83 | 0.77 |
| 600104 | 2.08 | 1.26 | 0.80 | 601390 | 1.26 | 0.84 | 0.73 |
| 600109 | 1.66 | 0.64 | 0.79 | 601398 | 1.93 | 1.32 | 0.80 |
| 600111 | 2.31 | 1.03 | 0.75 | 601601 | 3.00 | 1.14 | 0.83 |
| 600406 | 1.19 | 1.03 | 0.82 | 601628 | 1.83 | 0.97 | 0.76 |
| 600518 | 1.71 | 1.05 | 0.79 | 601668 | 1.75 | 0.94 | 0.76 |
| 600519 | 2.32 | 2.00 | 0.79 | 601688 | 2.11 | 1.00 | 0.80 |
| 600547 | 1.56 | 0.77 | 0.81 | 601766 | 1.72 | 0.96 | 0.75 |
| 600637 | 1.40 | 0.74 | 0.77 | 601788 | 1.43 | 0.78 | 0.80 |
| 600837 | 1.38 | 0.71 | 0.75 | 601800 | 1.66 | 0.84 | 0.78 |
| 600887 | 2.53 | 1.58 | 0.81 | 601818 | 1.59 | 0.99 | 0.82 |
| 600893 | 2.21 | 0.80 | 0.79 | 601857 | 1.38 | 0.89 | 0.73 |
| 600958 | 1.42 | 0.75 | 0.75 | 601901 | 1.44 | 0.76 | 0.79 |
| 600999 | 1.62 | 1.00 | 0.77 | 601985 | 1.27 | 0.93 | 0.79 |
| 601006 | 1.88 | 1.16 | 0.81 | 601988 | 1.73 | 1.07 | 0.82 |
| 601088 | 1.99 | 1.23 | 0.82 | 601989 | 1.33 | 0.69 | 0.86 |
| 601166 | 1.39 | 0.96 | 0.79 | 601998 | 1.73 | 0.93 | 0.79 |
小结
行文至此,我们不难发现本文提出的一种基于隐马尔科夫模型的股价涨跌区间预测方法对于确定投资时机有不错的适应性。从一开始的单一股票、确定时间的测试中,我们的实验模型比较有效地识别出了上涨与下跌的区间。虽然在一些上涨区间中混杂着下跌的某一两天,但是本文并不是要准确预测明日的涨跌。这些区间整体而言还是上涨的,即在区间开始时购买并在区间结束后卖出可以获得正收益。所以我们依旧可以认为其识别正确。其次在单一股票时间变动测试中我们希望解释此方法在时间维度上的普适性。在5000天的时间跨度中以300天为滑动窗口,结果表明,使用本文所述方法相比直接持有股票300天可以有效地提高投资收益,并且几乎不会出现投资亏损的情况。之后在上证50样本300天测试中我们希望解释此方法在股票种类维度上的普适性。由于直接选取所有上证股票样本过于繁杂,所以我们选取了比较有代表性的上证50样本股。通过与上一个测试相似的方法我们发现,对于这些样本,采用本文的方法都有效地提高了收益,且所有股票投资结果均显示正收益。这些结果都是令人欣喜地,三个实验很好的说明了本文所描述的方法无论在何种时期,无论对于何种股票,有具有不错的适应性。这似乎在告诉我们这个方法良好的应用前景。
局限性分析
从之前的分析来看,本文所说的一种基于隐马尔科夫模型的股价涨跌区间预测方法似乎好到无可挑剔。只要在一个较长的时间段内使用此方法似乎不但保本二期能达到近乎70%的年化收益率。而且无关乎股票的选择,无关乎投资开始的时间点。但事实上我们知道这种无风险超高回报的事情不应该存在于现实生活中。考虑到模型与现实之间的差距,我们将进行本方法的局限性分析。
实际问题
其实不难发现,本文只是一个买卖股票的理论模型,其中存在大量的简化,简化的内容将导致我们的收益上升,也就造成了我们所见的极其优秀的实验结果:
- 股票交易手续费:股票交易手续费就是指投资者在委托买卖证券时应支付的各种税收和费用的总和。由印花税、佣金、过户费等组成。
- 股票交易规则:股票的交易存在着一些规则,在这些规则是制约下,其实我们一般不会在我们预想的时间点用我们预想的价格买入或者卖出。
所以从实际的角度来看我们会遇到这样的问题,由于买卖手续费的存在,一次买卖只有超过7‰的价格上涨才开始有收益。我们其实可以想想一个这样的情况,通过本文的方法我们被提示了一个不错的买入点,此时的价格为10.00元,于是我们开始尝试买入,但是由于大家都看好这只股票,价格开始上涨,最终我们以10.02的价格买入,持有了一段时间后股票价格上涨到了10.10,此时我们的计算又告诉了我们后市不容乐观,在我们准备卖出时,大家的恐慌心理导致买单变少,我们不得不忍痛让利抛售,最终以10.08的价格清仓。从软件的角度它为我们寻找到了一段1%的价格上涨区间,但是实际操作的结果缺失损失了1‰。这就是理论与实践之间的巨大差别,所以本文所说的方法,我们只能表示问存在良好的应用前景。具体的实用性还是有待实际操作后的结果反馈。
参数估计问题
在本文中隐马尔科夫模型的参数我们统一使用了人为给定的两个参数矩阵:
\[转移概率矩阵=\begin{pmatrix} 0.6&0.4\\ 0.4&0.6\\ \end{pmatrix} 发射概率矩阵=\begin{pmatrix} 0.6&0.4\\ 0.4&0.6\\ \end{pmatrix}\]如此选取是因为我们设想的是股市的隐式序列两个状态——上涨区间与下跌区间之间存在一定的连续性,所以在自己本身状态之间的转移概率应该略高于两种状态之间的转化。而对于发射概率来说就更好理解了,对于上涨区间来说,自然是出现上涨的概率更高,反之亦然。但其实对于隐马尔科夫模型我们有Baum-Welch算法来让机器自动生成一个最优的参数矩阵。但是在实际操作中我们却遇到了一些棘手的问题。在自动优化的迭代步骤后,往往其转移最优概率将会出现1和0的组合,即只有上升区间或者只有下降区间。
推测可能的原因是我们设想的涨跌区间两种状态之间的差别十分微小。考虑这样一种极端的情况:长度为L的序列,显示序列表示为RBRB···RBRB这样的涨跌交替出现,对于隐式序列的两种极端情况唯一状态(DDDD···DDDD)和交替状态(UDUD···UDUD)都有最大概率${\frac{1}{2}}^L$。造成这一状况可能的原因是我们的数据指标太少,只考虑了上涨与否的一个布林指数来定义显式序列。事实上涨跌是存在幅度的:上涨5%与下跌0.5%交替出现与上涨0.5%与下跌5%交替出现两者在本文描述的显式序列定义下是一样的,但我们明显能感受到前者是一个上涨区间,后者是一个下跌区间。其次换手率,成交额,市值大小都是可以被考虑的指标。
小结
对于本文所描述的方法进行投资会遇到如上述的两个不足之处。其一是理论模型未考虑到现实投资股票时会遇到的各种费用和同质化预期对买卖价格的影响。这点造成了测试结果近乎完美的呈现,但是事实上我们知道这种零风险高收益的不可能存在的,对于具体造成的收益减少有多少只有通过实际资金的入市测试才有可能知道。限于客观条件我们只停留在程序模拟层面。如果以后有机会将进一步深入研究。其二就是参数估计问题,在本文中我们选取的都是人为根据我们的设想前提给定的概率矩阵,但事实上隐马尔科夫模型是配套有参数估计算法的,在此算法下我们的结果总是比较容易趋向于极端情况,推测是由于两种状态之间的实际差别没有那么大导致的,因此需要引入更多的指标来完善对于显示序列的描述,比如涨跌幅度,换手率等。
第三章 结论与展望
本文介绍了一种基于隐马尔科夫模型的股价涨跌区间预测方法,在此方法下我们可以科学地选择一只股票的买入与卖出时机,达到量化交易的效果。由于量化交易中的算法交易是根据事先设定好的算法控制选股与买卖所以有着系统性、纪律性和客观性,可以排除了人的主观错误判断和冲动造成的损失。在目前的股票交易市场成为了一种新兴的投资方式与理念。本文所述方法旨在关注与选股后买卖时间的把控,为投资者提供一个较好的买卖时机点。事实上我们在生活中也常常发现同一只股票不同的买卖时间点造成的巨大收益差距。通过Python编程,使用计算机模拟得到了良好的结果。单一股票定时测试而言,我们选取的股票在300天模拟中抵抗住了10%真实股价下跌带来的影响成功在300天后获得近40%的正收益。在此基础上我们拓宽本文方法在时间维度上的实用性,对上一步所测试的股票进行间隔50天固定300天窗口的时间变动测试,测试结果依旧十分理想。在充分长的时间内使用本文方法将使得收益明显高于其实际价格走势,且几乎保证了正收益。于是我们又拓展了本文方法在股票种类维度上的使用性,结果一样令人满意,以上证50中的50只股票为样本,300天测试后,对于所有股票,使用本文方法300天后价格均高于直接持有300天,且一样几乎保证了本金的安全性。至此测试几乎可以说是相当成功,本方法只要有差不多一年的连续使用,无论在什么时间,什么股票下都能提高收益且重要的是几乎保证了本金的安全降低风险。但事实上我们也只打,这种只有高收益没有风险的投资是不可能存在的,究其原因是因为本文的所有操作都只是计算机根据历史数据模拟的,而非真实入市。在真实情况中,每一次买卖都有各种费率的影响,只有超过0.7%的价格上涨才有正收益,频繁的买卖操作有时反而会消耗自己已有的利润。其次就是同质化预期,在一个股市中投资人往往会对后市做出同样的预期。这时你将难以在你原本想要购入的价格买到你想要的股票,被迫只能让利买卖,这一步同样蚕食了本文预测的收益。对于本文的理论方法而言,所有的测试中概率矩阵参数都是人为根据我们对股市存在一个隐式状态序列的假想大致给出的。而科学家对于隐马尔科夫序列的参数估计是有一个配套的算法解决的。但是实际操作中由于对显示状态的描述指标过少导致了两种隐式状态之间的差别太小,所以自动优化会区域一个局部最大值的极端而无法使用。
限于目前的知识水平与客观条件,此方法的研究只能停留在计算机模拟层面。如果以后有机会可以通过米筐测试小资金真实股市运作下的收益情况。
引用
[1]1 Baum, L. E.; Petrie, T. (1966). “Statistical Inference for Probabilistic Functions of Finite State Markov Chains”. The Annals of Mathematical Statistics. 37 (6): 1554–1563. doi:10.1214/aoms/1177699147. Retrieved 28 November 2011.
[2]1 Baum, L. E.; Eagon, J. A. (1967). “An inequality with applications to statistical estimation for probabilistic functions of Markov processes and to a model for ecology”. Bulletin of the American Mathematical Society. 73 (3): 360. doi:10.1090/S0002-9904-1967-11751-8. Zbl 0157.11101.
[3]1 Baum, L. E.; Sell, G. R. (1968). “Growth transformations for functions on manifolds”. Pacific Journal of Mathematics. 27 (2): 211–227. doi:10.2140/pjm.1968.27.211. Retrieved 28 November 2011.
[4]1 Baum, L. E.; Petrie, T.; Soules, G.; Weiss, N. (1970). “A Maximization Technique Occurring in the Statistical Analysis of Probabilistic Functions of Markov Chains”. The Annals of Mathematical Statistics. 41: 164. doi:10.1214/aoms/1177697196. JSTOR 2239727. MR 0287613. Zbl 0188.49603.
[5]1 Baum, L.E. (1972). “An Inequality and Associated Maximization Technique in Statistical Estimation of Probabilistic Functions of a Markov Process”. Inequalities. 3: 1–8.
[6]1 Stratonovich, R.L. (1960). “Conditional Markov Processes”. Theory of Probability and its Applications. 5 (2): 156–178. doi:10.1137/1105015.
[7]1 Thad Starner, Alex Pentland. Real-Time American Sign Language Visual Recognition From Video Using Hidden Markov Models. Master’s Thesis, MIT, Feb 1995, Program in Media Arts
[8]1 B. Pardo and W. Birmingham. Modeling Form for On-line Following of Musical Performances. AAAI-05 Proc., July 2005.
[9]1 Satish L, Gururaj BI (April 2003). “Use of hidden Markov models for partial discharge pattern classification”. IEEE Transactions on Dielectrics and Electrical Insulation.
[10] Pieczynski, Wojciech (2007). “Multisensor triplet Markov chains and theory of evidence”. International Journal of Approximate Reasoning. 45: 1–16. doi:10.1016/j.ijar.2006.05.001.
[11] Boudaren et al., M. Y. Boudaren, E. Monfrini, W. Pieczynski, and A. Aissani, Dempster-Shafer fusion of multisensor signals in nonstationary Markovian context, EURASIP Journal on Advances in Signal Processing, No. 134, 2012.
[12] Lanchantin et al., P. Lanchantin and W. Pieczynski, Unsupervised restoration of hidden non stationary Markov chain using evidential priors, IEEE Trans. on Signal Processing, Vol. 53, No. 8, pp. 3091-3098, 2005.
[13] Boudaren et al., M. Y. Boudaren, E. Monfrini, and W. Pieczynski, Unsupervised segmentation of random discrete data hidden with switching noise distributions, IEEE Signal Processing Letters, Vol. 19, No. 10, pp. 619-622, October 2012.
[14] “stock Definition”. Investopedia. Retrieved 25 February 2012
[15] “Understanding Stock Prices: Bid, Ask, Spread”. Youngmoney.com. Retrieved 2010-02-12.
